Here’s a simple, but effective proof that palindromes are not a regular language.

It’s known as the Myhill–Nerode theorem.

This can be proven by verifying that the check if string is a palindrome cannot be implemented using deterministic finite automaton (DFA). We will suppose that such DFA exists and then reach logical contradiction, thereby proving it cannot actually exist.

Proof:

Since there is an infinite number of strings and a finite number of DFA states, there have to exist two different strings that reach the same state (this is a logical conclusion, but it’s formally known as the pigeonhole principle).

Without loss of generality, we can pick some arbitrary representations for these strings:

A = “1234”, B = “5678”

Now:

• We posited that both inputs A and B reach the same state S1 in our DFA
• By appending the same character sequence C to each string, they will both reach some state S2 (DFA has no memory of input, it just follows the transitions from S1)
• Let’s take C = “321”.
  • For AC (“1234321”), end state S2 should be accepting
  • For BC (“5678321”), end state S2 should be non-accepting

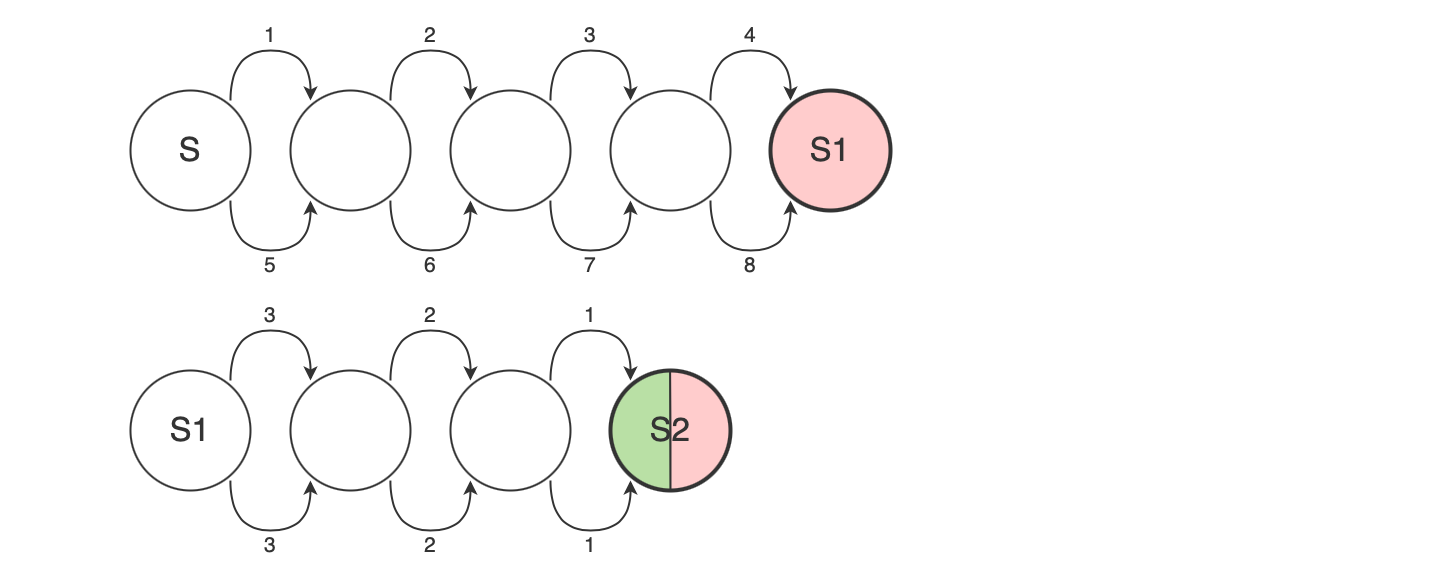
We reached a contradiction; S2 cannot be both accepting and non-accepting.